Überblick über einige elementare Funktionen
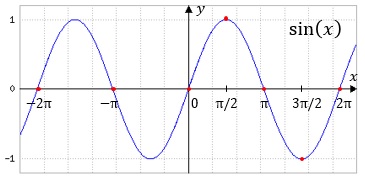
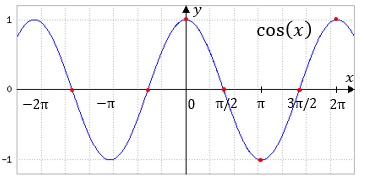
Die Winkelfunktionen sin(x) und cos(x)
|
|
|
Sie sollten sich die Graphen dieser beiden Funtkionen gut einprägen. Falls es Ihnen die bildliche Vorstellung schwer fällt, können Sie sich die Kurven auch mit einfachen Worten einprägen. Sowohl die Sinus- als auch die Kosinusfunktion schwingen zwischen den Werten -1 und +1 und haben beide die Periode 2π. Sinus fängt bei 0 und Kosinus bei 1 an. Daraus lässt sich alles Weitere rekonstruieren. Bei entsprechenden Abi-Aufgaben sollten Sie sich die Zeit nehmen und eine kleine Skizze zeichnen, so dass Sie bequem ablesen können.
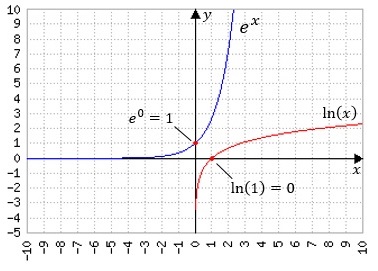
Die Exponentialfunktionen ex und der natürliche Logarithmus ln(x)
|
|
|
Hier sollten Sie sich merken, dass die e-Funktion nur positive Werte annimmt und somit niemals 0 wird.
Der natürliche Logarithmus hingegen kann alle Werte annehmen, also auch negative Werte sowie die 0, aber er ist nur für positive Werte definiert. Das bedeutet, dass man für x nur positive Werte einsetzen darf. Insbesondere ist ln(0) ist nicht definiert!
Wenn Sie also beispielsweise beim Auflösen einer Gleichung auf eine Gleichung wie etwa ex=0 oder x=ln(0) stoßen, so wissen Sie, dass dies nicht möglich ist.
Die Exponentialfunktion und der natürliche Logarithmus stehen in einem umgekehrten Verhältnis zueinander, d.h. sie heben sich gegenseitig auf, etwa so wie Wurzel und Quadrat.
Somit gilt eln(x)=x und ebenso ln(ex)=x.
Ein paar spezielle Kennwerte wie e0=1 und ln(1)=0 sollten Sie ebenfalls auswendig kennen.
| Downloads |
PowerPoint